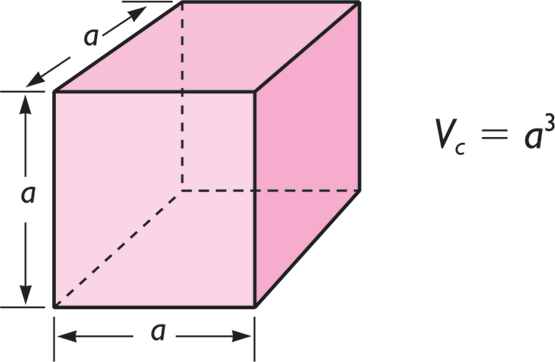
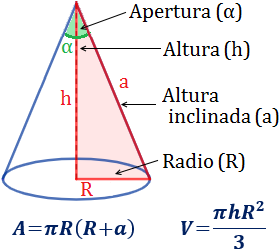
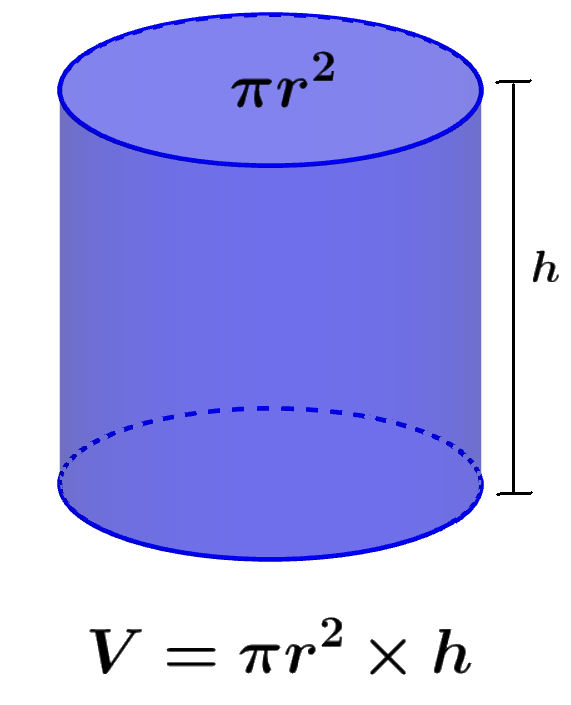
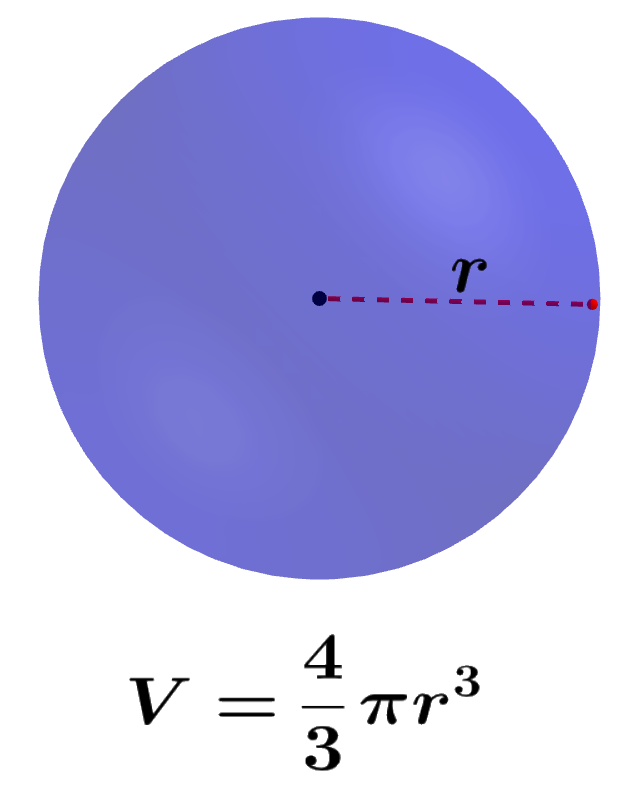
Rama de las matemáticas encargada de las propiedades y medida de la extensión de las formas que se pueden expresar con medidas y de las relaciones entre puntos, líneas, ángulos, planos y sólidos en el espacio para definir sus condiciones mediante unas propiedades determinadas del espacio. También llamada geometría del espacio
Un objeto o ente es tridimensional si tiene tres dimensiones. Es decir, cada uno de sus puntos puede ser localizado especificando tres números dentro de un cierto rango. Ejemplo: anchura, altura y profundidad.
Plano en el espacio